let x and y be the bags of brands P and Q respectively. Obviously x ≥ 0, y ≥ 0. Mathematical formulation of given problem is as follows:

Maximize Z = 3x + 3.5y ….(1)

Subject to the constraints,

x + 2y ≤ 240 …..(2)

3x + 1.5y ≤ 270 ⇒ x + 0.5y=90 …..(3)

1.5x + 2y ≤ 310 ….(4)

x ≥ 0, y ≥ 0 ….(5)

Now let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is bounded.

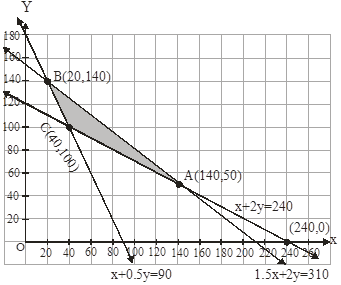
The coordinates of the corner points A(140,50),B(20,40) and C(40,100).

Now, we find the maximum value of Z. According to table the maximum value of Z = 595 at point A (140,50).

Hence, 140 and 50 be be the bags of brands P and Q respectively to be added to the garden to maximize the amount of nitrogen.