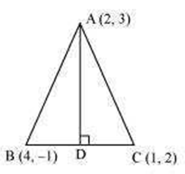
Let AD be the altitude of triangle ABC from vertex A.

Accordingly, AD is perpendicular to BC

Given vertices A (2, 3), B (4, –1) and C (1, 2)

Slope of line BC = m₁

m₁ = (- 1 - 2)/(4 - 1)

m₁ = -1

Let slope of line AD be m₂

AD is perpendicular to BC

∴ m₁ × m₂ = -1

⇒ -1 × m₂ = -1

∴ m₂ = 1

The equation of the line passing through point (2, 3) and having a slope of 1 is

⇒ y – 3 = 1 × (x – 2)

⇒ y – 3 = x – 2

⇒ y – x = 1

Equation of the altitude from vertex A = y – x = 1

Length of AD = Length of the perpendicular from A (2, 3) to BC

Equation of BC is

y + 1 = -1 × (x – 4)

⇒ y + 1 = -x + 4

⇒ x + y – 3 = 0 …………………(1)

Perpendicular distance (d) of a line Ax + By + C = 0 from a point (x₁, y₁) is given by

Comparing equation (1) to the general equation of line i.e., Ax + By + C = 0, we obtain

A = 1, B = 1 and C = -3

Length of AD =

The equation and the length of the altitude from vertex A are y – x = 1 and

√2 units respectively.