Let A (1, 3) and B (-4, 1) be the coordinates of the end points of the hypotenuse.

Now, potting the line segment joining the points A (1, 3) and B (-4, 1) on the coordinates plane, we will get two right triangles with AB as the hypotenuse. Now, from the graph, it is clear that the point of intersection of the other two legs of the right triangle having AB as the hypotenuse can either P or Q.

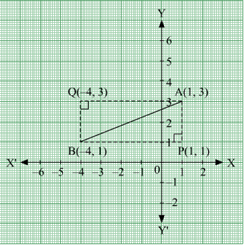
Now, when ΔAPB is taken.

The perpendicular sides in ΔAPB are AP and PB.

Now, sides PB is parallel to x – axis and at a distance of 1 units above x – axis.

So, equation of PB is, y = 1 or y -1 = 0.

The side AP is parallel to y – axis and at a distance of 1 units on the right of y – axis.

So, equation of AP is x = 1 or x - 1 = 0.

And when ΔAQB is taken.

The perpendicular sides in ΔAQB are AQ and QB.

Now, sides AQ is parallel to x – axis and at a distance of 3 units above x – axis.

So, equation of AQ is, y = 3 or y -3 = 0

The side QB is parallel to y – axis and at a distance of 4 units on the left of y – axis.

So, equation of QB is x = -4 or x +4 = 0.