A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.

Question

Philoid · Accepted Answer

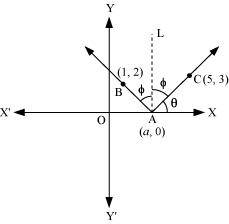
Let the coordinate of point A be (a, 0)

Draw a line (AL) perpendicular to the x –axis.

We know that angle of incidence is equal to angle of reflection. Hence, let

ɸ

Let Ɵ

Therefore,

0 –(Ɵ+2ɸ) = 180⁰ –[Ɵ+2(90⁰ - Ɵ)]

= 180⁰ – Ɵ+180⁰ +2Ɵ

= Ɵ

Thus, 0 – Ɵ

Now, slope of line AC =

------------ (1)

Slope of line AB =

----------------- (2)

From equations (1) and (2), we get,

⇒ 3a – 3 = 10 – 2a

⇒ a =

Therefore, the coordinates of point A are .