Given: ΔABC and ΔPQR, AB = AC, ∠C = ∠P and ∠B = ∠Q

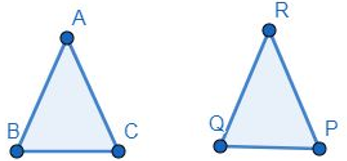
AB = AC

⇒ ∠B = ∠C (opposite angles to equal sides are equal)

Hence, ΔABC is an isosceles triangle.

∠C = ∠P and ∠B = ∠Q (given)

⇒ ∠P = ∠Q (∵∠B = ∠C)

⇒ QR = PR (opposite sides to equal angles are equal)

Hence, ΔPQR is an isosceles triangle.

So, the two triangles are isosceles but not congruent.

As AAA is not the criterion for a triangle to be congruent.

Hence, option A is correct.