Q is a point on the side SR of a ΔPSR such that PQ = PR. Prove that PS PQ.

Question

Q is a point on the side SR of a ΔPSR such that PQ = PR. Prove that PS > PQ.

Philoid · Accepted Answer

Given: in ΔPSR, Q is a point on the side SR such that PQ = PR.

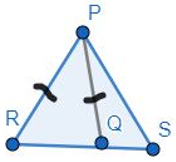
In ΔPRQ,

PR = PQ (given)

⇒ ∠PRQ = ∠PQR (opposite angles to equal sides are equal)

But ∠PQR > ∠PSR (exterior angle of a triangle is greater than each of opposite interior angle)

⇒ ∠PRQ > ∠PSR

⇒ PS > PR (opposite sides to greater angle is greater)

⇒ PS > PQ (as PR = PQ)