Given: Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O.

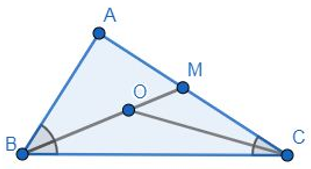
In ΔABC,

AB = AC (given)

⇒ ∠ACB = ∠ABC (opposite angles to equal sides are equal)

1/2 ∠ACB = 1/2 ∠ABC (divide both sides by 2)

⇒ ∠OCB = ∠OBC …(1) (As OB and OC are bisector of ∠B and ∠C)

Now, ∠MOC = ∠OBC + ∠OCB (as exterior angle is equal to sum of two opposite interior angle)

⇒∠MOC = ∠OBC + ∠OBC (from (1))

⇒ ∠MOC = 2∠OBC

⇒∠MOC = ∠ABC (because OB is bisector of ∠B)

Hence proved.