The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

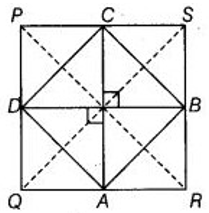
∵ ABCD is a rhombus

∴ AB = BC = CD = DA

Now,

∵ D and C are midpoints of PQ and PS

∴ DC = 1/2QS [By midpoint theorem]

Also,

∵ B and C are midpoints of SR and PS

∴ BC = 1/2PR [By midpoint theorem]

∵ ABCD is a rhombus

∴ BC = CD

⇒ 1/2QS = 1/2PR

⇒ QS = PR

Hence, diagonals of PQRS are equal