If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form

Question

Philoid · Accepted Answer

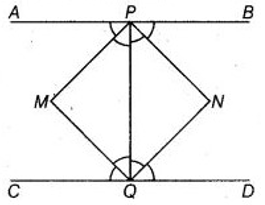
Let the bisectors of the angles APQ and CQP meet at M and bisectors of the angles BPQ and PQD meet at N.

Join PM, MQ, QN and NP.

∠APQ = ∠PQD [∵APB ∥ CQD]

⇒ 2∠MPQ = 2∠NQP [∵ NP and PQ are angle bisectors]

Dividing both sides by 2,

⇒ ∠MPQ = ∠NQP

⇒ PM ∥ QN

Similarly,

⇒ ∠BPQ = ∠CQP

⇒ PN ∥ QM

∴ PNQM is a parallelogram

Now,

∠CQP + ∠CQP = 180° [Angles on a straight line]

⇒ 2∠MQP + 2∠NQP = 180°

Dividing both sides by 2,

⇒ ∠MQP + ∠NQP = 90°

⇒ ∠MQN = 90°

Hence, PMQN is a rectangle