In Fig. 8.7, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Question

In Fig. 8.7, P is the mid-point of side BC of a parallelogram ABCD such that ∠ BAP = ∠ DAP. Prove that AD = 2CD.

Philoid · Accepted Answer

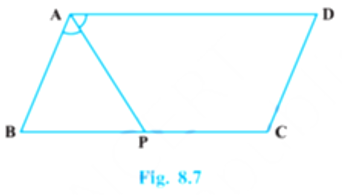
Since ABCD is a parallelogram, AD||BC and AB is a transversal.

(Sum of co-interior angles is 180)

In ΔABP,

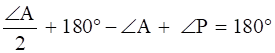
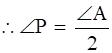
(opposite sides of equal angles are equal)

Now, multiply both sides by 2, we get,

(P is mid-point of BC)

(AB||CD and AD||BC)

Hence, Proved.