A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.

Question

Philoid · Accepted Answer

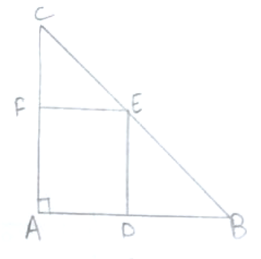
Given, ΔABC with ∠A = 90 and

AB = AC …(i)

Let ADEF is a square,

AD = AF = EF = AD …(ii)

Subtracting eqn (ii) from (i),

AB-AD = AC-AF

BD = CF

Now, in ΔCFE and ΔEDB,

BD = CF

DE = EF

∠CFE = ∠EDB = 90 (Side of square)

ΔCEF BED (By SAS)

CE = BE

Hence, vertex E of the square bisect the hypotenuse BC.