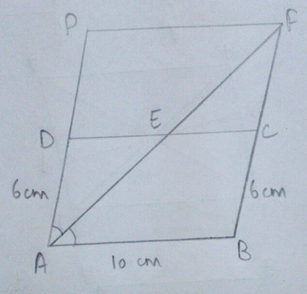
Given, AB = 10 cm, AD = 6 cm
DC = AB = 10 cm and AD = BC = 6 cm
Given, bisector of ∠A intersects DE at E and BC produced at F.
Now, drawing PF || CD.
From the figure, CD || FP and CF || DP
PDCF is a parallelogram.
And , AB || FP and AP || BF
ABFP is also a parallelogram
In ΔAPF and ΔABF
∠APF = ∠ABF (opposite angles of a parallelogram are equal)
AF = AF (Common side)
∠PAF = ∠AFB (Alternate angles)
ΔAPF ≅ ΔABF (By ASA congruence criterion)
AB = AP (CPCT)
AB = AD + DP
= AD + CF (Since DCFP is a parallelogram)
∴ CF = AB – AD
= (10 – 6) cm = 4 cm