P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.

Question

Philoid · Accepted Answer

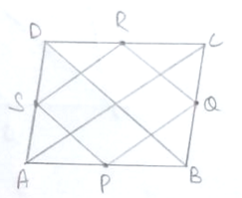
Given, P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively.

Also, AC = BD.

In ΔADC, by mid-point theorem,

SR||AC and SR = AC

In ΔABC, by mid-point theorem,

PQ||AC and PQ = AC

SR = PQ = AC

Similarly,

In ΔBCD, by mid-point theorem,

RQ||BD and RQ = BD

In ΔBAD, by mid-point theorem,

SP||BD and SP = BD

SP = RQ = BD = AC

So,

SR = PQ = SP = RQ

Hence, PQRS is a rhombus.