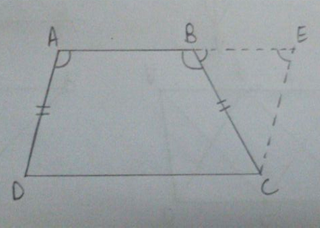
Given, ABCD is a quadrilateral in which AB || DC and AD = BC.

Extend AB to E and draw a line CE parallel to AD.

Since AD||CE and transversal AE cuts them at A and E, respectively.

∠A + ∠E = 180

∠A = 180-∠E

Since, AB||CD and AD||CE

So quadrilateral AECD is a parallelogram.

Now, AD = CE BC = CE

In ΔBCE,

CE = BC

∠CBE = ∠CEB (opposite angles of equal sides are equal)

180-∠B = ∠E

180-∠E = ∠B

∠A = ∠B

Hence, proved.