Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
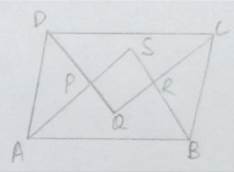
Let ABCD is a parallelogram.
Since, DC||AB and DA is transversal.
![]() ∠A + ∠D = 180
∠A + ∠D = 180![]()
 ∠A +
∠A +  ∠D = 90
∠D = 90![]()
∠PAD + ∠PDA = 90![]()
∠APD = 90![]()
![]() ∠SPQ = 90
∠SPQ = 90![]()
Similarly, ∠PQR = 90![]() , ∠QRS = 90
, ∠QRS = 90![]()
And ∠PSR = 90![]()
Thus, PQRS is a quadrilateral each of whose angles is 90![]() .
.
Hence, PQRS is a rectangle.
13