P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
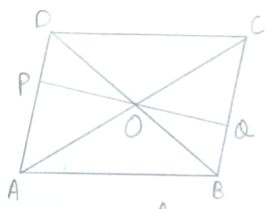
Given, ABCD is a parallelogram whose diagonals bisect each other at O.
Now, in ΔODP and ΔOBQ,
∠BOQ = ∠POD
∠OBQ = ∠ODP (AD||BC and BD is transversal)
![]() OB = OD
OB = OD
![]()
![]() OP = OQ
OP = OQ
Hence, O bisect PQ.
14