AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the center of the circle is :
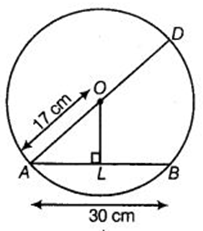
Given: Diameter of the circle = d = AD = 34 cm
∴ Radius of the circle = r = d/2 = AO = 17 cm
Length of chord AB = 30 cm
Since the line drawn through the center of a circle to bisect a chord is perpendicular to the chord, therefore AOL is a right angled triangle with L as the bisector of AB.
∴ AL = 1/2(AB) = 15 cm
In right angled triangle AOB, by Pythagoras theorem, we have:
(AO)2 = (OL)2 + (AL)2
⇒ (17)2 = (OL)2 + (15)2
⇒ (OL)2 = (17)2 - (15)2
⇒ (OL)2 = 289 – 225
⇒ (OL)2 = 64
Take square root on both sides:
⇒ (OL) = 8
∴ The distance of AB from the center of the circle is 8 cm.
3