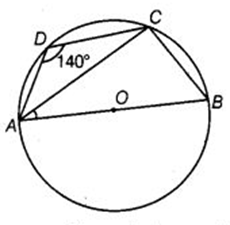
Given: ABCD is a cyclic quadrilateral.

∠ADC = 140°

Since sum of opposite angles of a cyclic quadrilateral is 180°,

∴ ∠ADC + ∠ABC = 180°

⇒ 140° + ∠ABC = 180°

⇒ ∠ABC = 180° - 140°

⇒ ∠ABC = 40°

Since, diameter subtends a right angle to the circle,

∴ ∠ACB = 90°

Now, in triangle ACB; by angle sum property of a triangle, sum of all angles of a triangle is 180°.

∴ ∠CAB + ∠ABC + ∠ACB = 180°

⇒ ∠CAB + 40° + 90° = 180°

⇒ ∠CAB = 180° - 90° - 40°

⇒ ∠CAB = 50°

∴ ∠CAB = ∠50°