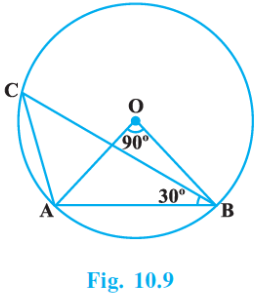
Given: ∠AOB = 90°, ∠ABC = 30°

OA and AB are radius and are equal,

∴ ∠OAB = ∠OBA = x (say) (∵ angles opposite to equal sides are equal)

In triangle OAB, using the angle sum property, sum of all angles of triangle is 180°.

∴ ∠AOB + ∠OAB + ∠OBA = 180°

⇒ 90° + x + x = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = 45°

∴ ∠OAB = ∠OBA = 45°

Since angles in the same segment are equal, therefore

∠ACB = ∠OAB = 45° (∵ ∠OAB = 45° and these angles lie in the same segment CB)

Now, in triangle CAB, using the angle sum property of triangle, sum of all angles is 180°.

∴ ∠CAB + ∠ABC + ∠BCA = 180°

⇒ ∠CAB + 30° + 45° = 180°

⇒ ∠CAB = 180° - 30° - 45°

⇒ ∠CAB = 105°

⇒ ∠CAO + ∠OAB = 105° (∵ ∠CAB = ∠CAO + ∠OAB)

⇒ ∠CAO + 45° = 105°

⇒ ∠CAO = 105° - 45°

⇒ ∠CAO = 60°

∴ ∠CAO = 60°