Let AB and CD be the chords of the circle with center O.

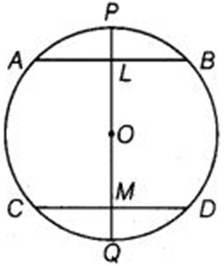
Let L and M be the mid points of AB and CD respectively and PQ is the line passing through these midpoints and the center of the circle. Therefore PQ is the diameter of the circle.

Since M is the midpoint of CD,

∴ OM ⊥ CD (because line joining center to the midpoint of a chord is always perpendicular to the chord.)

⇒ OMD = 90°

Similarly, L is the midpoint of AB,

∴ OL ⊥ AB (because line joining center to the midpoint of a chord is always perpendicular to the chord.)

⇒ OLA = 90°

But ∠OLA and ∠OMD are alternate angles, so AB ∥ CD.

Hence, proved.