If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are con cyclic.

Question

Philoid · Accepted Answer

Let O be the center of BC.

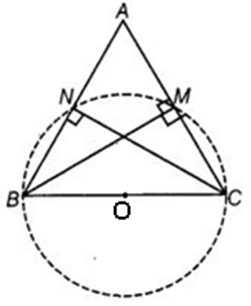
Since CN is perpendicular on AB, therefore ΔBNC is right angled triangle.

Therefore the circle passing through B, N and C will have midpoint of BC as center and OB be the radius. …………… (1)

Similarly, BM is perpendicular on AC, therefore ΔBMC is right angled triangle.

Therefore the circle passing through B, M and C will have midpoint of BC as center and OB be the radius. …………… (2)

From (1), we get a circle passing through B, N and C which is centered at O and has radius OB.

From (2), we get a circle passing through B, M and C which is centered at O and has radius OB.

Since from a fixed point and fixed radius, only one circle can be drawn. Therefore, same circle will pass through the four points B, M, N and C.

Therefore; B, N, M and C are concyclic.