Given: ABC is an isosceles triangle such that AB = AC and ED ∥ BC.

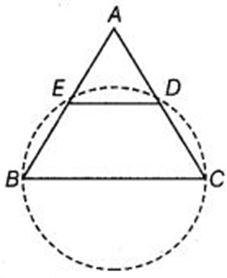
To prove: Quadrilateral BCDE is cyclic, ie. sum of opposite angles is 180°.

In ΔABC,

AB = AC (Equal sides of the isosceles triangle)

⇒ ∠ABC = ∠ACB (angles opposite to equal sides are equal)

As ED ∥ BC, therefore,

∠ADE = ∠ACB (corresponding angles)

Adding ∠EDC on both sides, we get:

∠ADE + ∠EDC = ∠ACB + ∠EDC

⇒ 180° = ∠ACB + ∠EDC

⇒ 180° = ∠ABC + ∠EDC (∵ ∠ACB = ∠ABC)

Sum of opposite angles of quadrilateral is 180°.

⇒ Quadrilateral BCDE is cyclic.

Hence, proved.