Given: ∠ACB = 40°

Since, the angle subtended by an arc at the center of a circle is twice the angle subtended by it at remaining part of the circle, therefore we have:

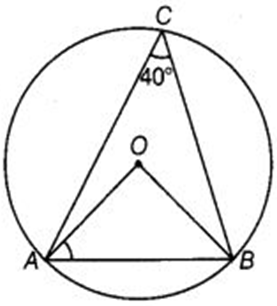
∠AOB = 2 × ∠ACB

= 2 × 40°

= 80°

Now, in triangle AOB, AO and BO are both radius of the circle.

Therefore, ∠OAB = ∠OBA = x (say) (angles opposite to equal sides are equal)

Using the angle sum property of triangle, sum of all angles of a triangle is 180°, we have:

∠OAB + ∠OBA + ∠AOB = 180°

⇒ x + x + 80° = 180°

⇒ 2x = 100

⇒ x = 50°

⇒ ∠OAB = 50°