Let the given triangle be ΔABC.

Then, given, ∠B = 45° and ∠C = 120° and AB + BC + CA = 10.4 cm.

Steps of Construction:

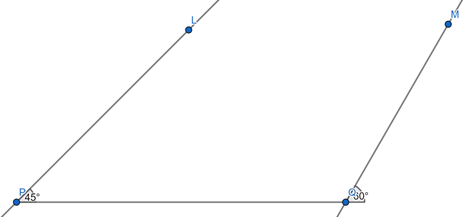
(i) Draw a line segment PQ = 10.4 cm.

(ii) Draw ray PL making an ∠LPQ = 45° at P and ray QM making an ∠MQP = 120° at Q.

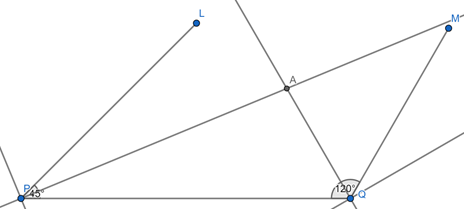
(iii) Bisect the ∠LPQ and ∠MQP. Let the intersection point of these bisectors be A.

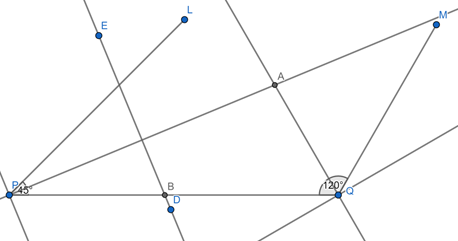
(iv)Draw the perpendicular bisector ED of AP, which intersect PQ at B.

(v)Draw another perpendicular bisector FG of AQ, which intersect PQ at C.

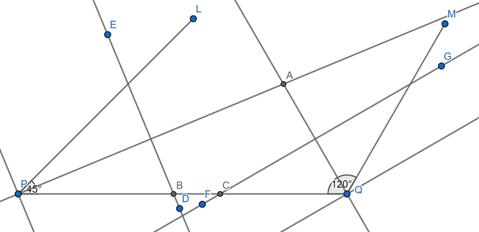
(vi) Join AB and AC.

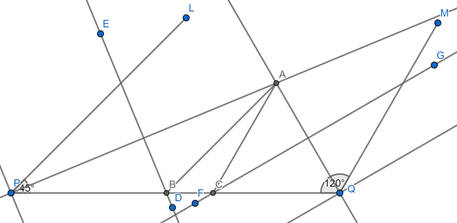
Thus, ABC is the required triangle.

Justification:

Since, B lies on the perpendicular bisector ED of AP.

So, AB = BP, then ∠APB = ∠PAB.

Similarly, C lies on the perpendicular bisector FG of AQ.

∴ AC = CQ, then ∠AQC = ∠QAC

Now, BC + CA + AB = BC + CQ + BP = PQ

And ∠ABC = ∠APB + ∠PAB = 2 ∠APB

= ∠LPQ = 45°

Similarly, ∠ACB = ∠AQC + ∠QAC = 2 ∠AQC

= ∠MQP = 120°

Thus, the construction is justified.