Steps of Construction:

(i) Draw the base, QR = 3 cm.

At point B, draw a ray QX, which makes ∠RQX = 45°

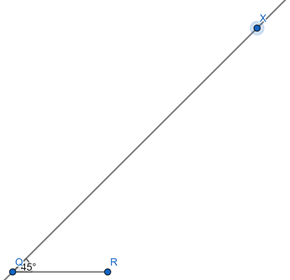
(ii) Here, QP – QR = 2 cm

∴ QP > QR

Hence, cut the line segment QD is equal to QP – QR = 2 cm from the ray QX.

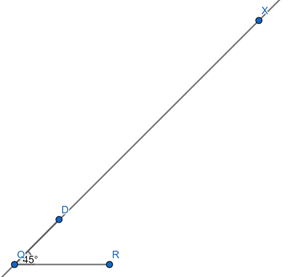
(iii) Now, join RD and draw its perpendicular bisector AB, which bisects RD at M (say).

Let P be the intersection point of perpendicular bisector AB and ray QX. Join PR.

Thus, ΔPQR is the required triangle.

Justification:

Base QR and ∠Q are drawn as given. Since, the point P lies on the perpendicular bisector of DR.

∴ PD = PR

QD = PQ – PD

⇒ QD = QP – QR

Thus, the construction is justified.