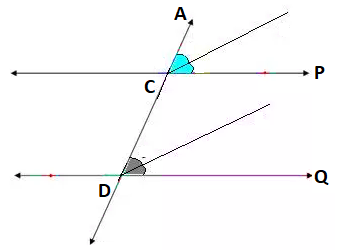
Let us draw the figure as below –

The two parallel lines are PR and QT.

Line A intersects P and Q at points C and D respectively.

Let CB and DE be the bisectors of ∠ACR and ∠ADT respectively.

We have to prove that CB and DE are parallel to each other.

We know, if two lines are parallel to each other, the corresponding angles are equal.

⇒

Dividing both sides by 2,

⇒

⇒

Now, we have two lines CB and DE such that the corresponding angles, ∠ACB and ∠CDE are equal.

Thus, CB || DE

Therefore, it is proved that the bisectors of any pair of corresponding angles so formed are parallel.