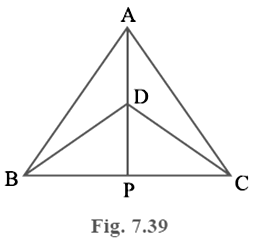
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅Δ ACD
(ii) Δ ABP ≅Δ ACP
(iii) AP bisects ∠ A as well as ∠ D.
(iv) AP is the perpendicular bisector of BC.
It is given in the question that:
are two isosceles triangles
(i) In 
,
AD = AD (Common)
AB = AC (Triangle ABC is isosceles)
BD = CD (Triangle DBC is isosceles)
Therefore,
By SSS axiom,
(ii) In 
AP = AP (Common)
∠PAB = ∠PAC (By c.p.c.t)
AB = AC (Triangle ABC is isosceles)
Therefore,
By SAS axiom,
(iii) ∠PAB = ∠PAC (By c.p.c.t)
AP bisects ∠A (i)
Also,
In 
PD = PD (Common)
BD = CD (Triangle DBC is isosceles)
BP = CP (
so by c.p.c.t)
Therefore,
By SSS axiom,
∠BDP = ∠CDP (By c.p.c.t) (ii)
By (i) and (ii), we can say that AP bisects ∠A as well as ∠D
(iv) ∠BPD = ∠CPD (By c.p.c.t)
And,
BP = CP (i)
Also,
∠BPD + ∠CPD = 180o (BC is a straight line)
2∠BPD = 180o
∠BPD = 90o (ii)
From (i) and (ii), we get
AP is the perpendicular bisector of BC