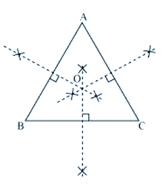
ABC is a triangle. Locate a point in the interior of Δ ABC which is equidistant from all the vertices of Δ ABC.
Circum centre of a triangle is always equidistant from all the vertices of that particular triangle.
Circum centre is the point where perpendicular bisectors of all the sides of the triangle meet together.
In ∆ABC, we can find the circum centre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle.
O is the point where these bisectors are
meeting together.
Therefore,
O is the point which is equidistant from all the vertices of ∆ABC
4