Let us consider a quadrilateral ABCD in which the diagonals AC and BD intersect each other at O.

It is given that the diagonals of ABCD are equal and bisect each other at right angles. Therefore, AC = BD, OA = OC, OB = OD, and

∠AOB = ∠BOC = ∠COD = ∠AOD = 90⁰

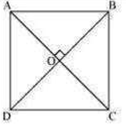
To prove ABCD is a square, we have to prove that ABCD is a parallelogram,

AB = BC = CD = AD, and one of its interior angles is 90⁰

In ΔAOB and ΔCOD,

AO = CO (Diagonals bisect each other)

OB = OD (Diagonals bisect each other)

∠AOB = ∠COD (Vertically opposite angles)

ΔAOB ΔCOD (SAS congruence rule)

AB = CD (By CPCT) (1)

And,

∠OAB = ∠OCD (By CPCT)

However, these are alternate interior angles for line AB and CD and alternate interior angles are equal to each other only when the two lines are parallel

AB || CD (2)

From equations (1) and (2), we obtain ABCD is a parallelogram

In ΔAOD and ΔCOD,

AO = CO (Diagonals bisect each other)

∠AOD = ∠COD (Given that each is 90⁰)

OD = OD (Common)

ΔAOD ΔCOD (SAS congruence rule)

AD = DC (3)

However,

AD = BC and

AB = CD (Opposite sides of parallelogram ABCD)

AB = BC = CD = DA

Therefore, all the sides of quadrilateral ABCD are equal to each other.

In ΔADC and ΔBCD,

AD = BC (Already proved)

AC = BD (Given)

DC = CD (Common)

ΔADC ΔBCD (SSS Congruence rule)

∠ADC = ∠BCD (By CPCT)

However,

∠ADC + ∠BCD = 180⁰ (Co-interior angles)

∠ADC + ∠ADC = 180⁰

2 ∠ADC = 180⁰

∠ADC = 90⁰ One of the interior angles of quadrilateral ABCD is a right angle.

Thus, we have obtained that ABCD is a parallelogram, AB = BC = CD = AD and one of its interior angles is 90⁰

Therefore, ABCD is a square