The figure is given below:

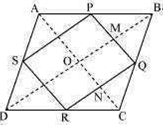
In ΔABC, P and Q are the mid-points of sides AB and BC respectively,

∴ From the mid-point theorem,

PQ || AC & PQ = ½ AC ..(1)

Also, R and S are the mid-points of CD and AD respectively

∴ From the mid-point theorem,

RS || AC & RS = ½ AC ..(2)

Therefore,

From equations (1) and (2), we obtain

PQ || RS and PQ = RS

Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other it is a parallelogram

Let the diagonals of rhombus ABCD intersect each other at point O

In quadrilateral OMQN,

MQ || ON (Because PQ || AC)

QN|| OM (Because QR || BD)

Therefore,

OMQN is a parallelogram

∠MQN = ∠NOM

∠PQR = ∠NOM

However, NOM = 90⁰ (Diagonals of a rhombus are perpendicular to each other)

PQR = 90⁰

Clearly, PQRS is a parallelogram having one of its interior angles as 90⁰

Hence, PQRS is a rectangle