ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.

Question

Philoid · Accepted Answer

Let EF intersect DB at G

By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side

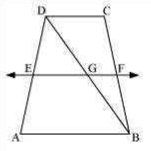
In ΔABD,

EF || AB and E is the mid-point of AD

Therefore,

G will be the mid-point of DB

EF || AB and

AB || CD

EF || CD (Two lines parallel to the same line are parallel to each other)

In ΔBCD,

GF || CD and

G is the mid-point of line BD. Therefore, by using converse of mid-point theorem, F is the mid-point of BC