(i) Let us draw a line segment EF, passing through point P and parallel to line segment AB

In parallelogram ABCD,

AB || EF (By construction) ... (i)

ABCD is a parallelogram

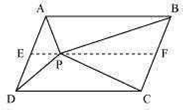
AD || BC (Opposite sides of a parallelogram)

AE || BF ... (ii)

From equations (i) and (ii), we get

AB || EF and

AE || BF

Therefore,

Quadrilateral ABFE is a parallelogram.

It can be observed that ΔAPB and parallelogram ABFE are lying on the same base AB and between the same parallel lines AB and EF

Therefore,

Area of triangle APB = * Area (ABFE) (iii)

Similarly,

For triangle PCD and parallelogram EFCD,

Area of triangle PCD = * Area (EFCD) (iv)

Adding (iii) and (iv), we get

Area of triangle APB + Area of triangle PCD = [Area (ABFE) + Area (EFCD)]

Area of triangle APB + Area of triangle PCD = Area (ABCD) (v)

(ii) Let us draw a line segment MN, passing through point P and parallel to line segment AD

In parallelogram ABCD,

MN || AD (By construction) (vi)

ABCD is a parallelogram

AB || DC (Opposite sides of a parallelogram)

AM || DN (vii)

From equations (vi) and (vii), we get

MN || AD and

AM || DN

Therefore,

Quadrilateral AMND is a parallelogram.

It can be observed that ΔAPD and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN

Area (ΔAPD) = Area (AMND) (viii)

Similarly,

For ΔPCB and parallelogram MNCB,

Area (ΔPCB) = Area (MNCB) (ix)

Adding equations (viii) and (ix), we get

Area (ΔAPD) + Area (ΔPCB) = [Area (AMND) + Area (MNCB)]

Area (ΔAPD) + Area (ΔPCB) = Area (ABCD) (x)

On comparing equations (v) and (x), we get

Area (ΔAPD) + Area (ΔPBC) = Area (ΔAPB) + Area (ΔPCD)