In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
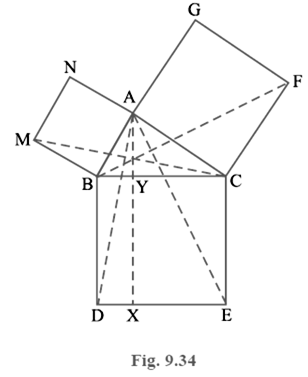
(i) Δ MBC ≅Δ ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) Δ FCB ≅Δ ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X
(i) Since, each angle of a square is 900
Hence, angle ABM = angle DBC = 900
ABM + ABC = DBC + ABC
MBC = ABD (1)
In ΔMBC and ΔABD,
Angle MBC = Angle ABD (From 1)
MB = AB (Sides of square)
BC = BD (Sides of square)
Therefore,
By SAS congruence rule,
![]()
(ii) Now, we have:
![]()
And we know that adjacent sides of square are perpendicular to each other. Hence,
BD perpendicular DE
And,
AX perpendicular DE
Also,
We know that two lines perpendicular to the same line are parallel to each other.
Therefore,
BD ‖ AX
Now,
![]() =
= ![]() (
(![]() and ‖gm BXYD are on same base BD and between the same parallels BD and AX)
and ‖gm BXYD are on same base BD and between the same parallels BD and AX)
Area (BXYD) = 2 area (ΔABD)
Area (BXYD) = 2 area (ΔMBC) (2)
(iii) ΔMBC and parallelogram ABMN are on same base MB and between the same parallels MB and NC.
Therefore,
Area (ΔMBC) = � ar (ABMN)
2 Area (ΔMBC) = Area (ABMN) = Area(BXYD) (From 2) (3)
(iv) Since, each angle of square is 900
Therefore,
Angle FCA = Angle BCE = 900
FCA + ACB = BCE + ACB
Angle FCB = Angle ACE
Now,
In ΔFCB and ΔACE,
Angle FCB = Angle ACE
FC = AC (Sides of square)
CB = CE (Sides of square)
Therefore,
By SAS congruence,
![]()
(v) It is given that AX is perpendicular to DE and CE is perpendicular to DE
and,
We know that two lines perpendicular to the same line are parallel to each other.
Hence,
CE ‖ AX
Now,
ΔACE and parallelogram CYXE are on same base CE and between the same parallels CE and AX.
Therefore,
Area (ΔACE) = 1/2 Area (CYXE)
Area (CYXE) = 2 Area (ΔACE) (4)
We had proved that
ΔFCB ![]() ΔACE
ΔACE
Hence,
Area (ΔACE) =Area (ΔFCB) (5)
Comparing 4 and 5, we get:
CYXE = 2 Area (ΔFCB) (6)
(vi) ΔFCB and parallelogram ACFG are on same base CF and between the same parallels CF and BG
Hence,
Area (ΔFCB) = � Area (ACFG)
Area (ACFG) = 2 Area (ΔFCB) = Area (CYXE) (Using 6) (7)
(vii) From figure:
Area (BCED) = Area (BXYD) + Area (CYXE)
Area (BCED) = Area (ABMN) + Area (ACFG) (using 3 and 7)