Let two circles with centres O and O' respectively intersect at two points A and B such that AB is the common chord of two circles and OO' is the line segment joining the centres, as shown in the figure: 

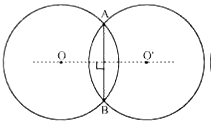
Also, AB is the chord of the circle centered at O. Therefore, the perpendicular bisector of AB will pass through O

Let OO' intersect AB at M. Also, draw line segments OA, OB, O'A and O'B

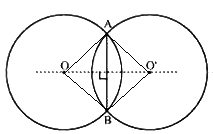
Now, In ΔOAO' and OBO',
OA = OB (radii of same circle)
O'A = O'B (radii of same circle)
O'O ( common side)
⇒ ΔOAO' ≅ ΔOBO' (Side-Side-Side congruency)
⇒ ∠AOO' = ∠BOO'
⇒ ∠AOM = ∠BOM ......(i)

Now in ΔAOM and ΔBOM we have
OA = OB (radii of same circle)
∠AOM = ∠BOM (from (i))
OM = OM (common side)
⇒ ΔAOM ≅ ΔBOM (Side-Angle-Side congruency)
⇒ AM = BM and ∠AMO = ∠BMO
But
∠AMO + ∠BMO = 180°
⇒ 2∠AMO = 180°
⇒ ∠AMO = 90°
Thus, AM = BM and ∠AMO = ∠BMO = 90°
Hence OO' is the perpendicular bisector of AB.