A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
The figure is shown as:
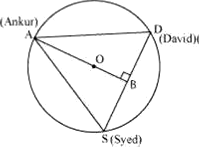
It is given that AS = SD = DA
⇒ ΔASD is an equilateral triangle
Now, OA (radius) = 20 m
And, the medians of an equilateral triangle pass through the circumcentre (O) of the equilateral triangle ASD.
Now, We also know that medians intersect each other in the ratio 2: 1.
As, AB is the median of equilateral triangle ASD,
∴ OA/OB = 2/1
⇒ 20m/OB = 2/1
⇒ OB = (20/2)m
⇒ OB = 10 m
Now, AB = OA + OB
⇒ AB = (20 + 10) m
⇒ AB = 30 m
Now, In ΔABD,
AD2 = AB2 + BD2
⇒ AD2 = (30)2 + (SD/2)2
⇒ AD2 = (30)2 + (AD/2)2
(Because AS = SD = DA in the equilateral triangle)
⇒ AD2 = 900 + (1/4)AD2
⇒ AD2 - (1/4)AD2 = 900
⇒ (3/4)AD2 = 900
⇒ AD2 = 1200
⇒ AD = 20√3 m
Therefore, the length of the string of each phone will be 20√3 m