ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.

Question

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If &#x2220; DBC = 70&#xB0;, &#x2220; BAC is 30&#xB0;, find &#x2220; BCD. Further, if AB = BC, find &#x2220; ECD.

Philoid · Accepted Answer

For chord CD,

∠CBD = ∠CAD (Angles in the same segment)

∠CAD = 70^o

∠BAD = ∠BAC + ∠CAD

= 30^o + 70^o

= 100^o

∠BCD + ∠BAD = 180° (Opposite angles of a cyclic quadrilateral)

∠BCD + 100^o = 180^o

∠BCD = 80^o

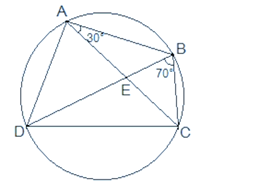
In ΔABC,

AB = BC (Given)

BCA = CAB (Angles opposite to equal sides of a triangle)

∠BCA = 30°

We have,

∠BCD = 80°

∠BCA + ∠ACD = 80°

30° + ∠ACD = 80°

∠ACD = 50°

∠ECD = 50°

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.