If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Question

Philoid · Accepted Answer

Let ABCD be a cyclic quadrilateral having diagonals BD and AC, intersecting each other at point O

∠BAD = ∠BOD

=

= 90^o

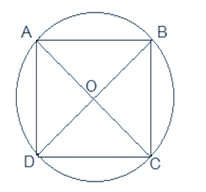
∠BCD + ∠BAD = 180° (Cyclic quadrilateral)

Consider BD as a chord

∠BCD = 180° − 90° = 90°

∠ADC = ∠AOC

= * 180^o

= 90^o

∠ADC + ∠ABC = 180° (Cyclic quadrilateral)

90° + ∠ABC = 180°

∠ABC = 90^o

Each interior angle of a cyclic quadrilateral is of 90°. Hence, it is a rectangle