Consider a trapezium ABCD with

AB | |CD and

BC = AD

Draw AM perpendicular to CD and BN perpendicular to CD

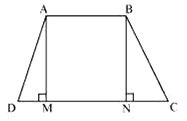
In ΔAMD and ΔBNC,

AD = BC (Given)

∠AMD = ∠BNC (By construction, each is 90°)

AM = BM (Perpendicular distance between two parallel lines is same)

ΔAMD ΔBNC (RHS congruence rule)

∠ADC = ∠BCD (CPCT) (i)

BAD and ADC are on the same side of transversal AD

∠BAD + ∠ADC = 180° (ii)

∠BAD + ∠BCD = 180° [Using equation (i)]

This equation shows that the opposite angles are supplementary

Therefore, ABCD is a cyclic quadrilateral