(i) Let p (x) = x³ – 2x² – x + 2

Factors of 2 are ±1 and ±2

By trial method, we find that

p (1) = 0

So, (x + 1) is a factor of p (x)

Now,

p (x) = x³ – 2x² – x + 2

p (-1) = (-1)³ – 2 (-1)² – (-1) + 2

= -1 – 2 + 1 + 2 = 0

Therefore, (x + 1) is the factor of p (x)

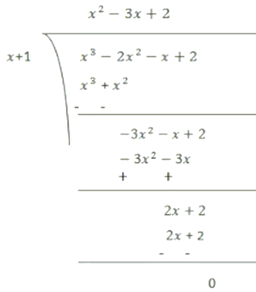
Now, Dividend = Divisor * Quotient + Remainder

(x + 1) (x² – 3x + 2)

= (x + 1) (x² – x – 2x + 2)

= (x + 1) {x (x – 1) – 2 (x – 1)}

= (x + 1) (x – 1) (x + 2)

(ii) Let p (x) = x³ – 3x² – 9x – 5

Factors of 5 are ±1 and ±5

By trial method, we find that

p (5) = 0

So, (x – 5) is a factor of p(x)

Now,

p (x) = x³ – 2x² – x + 2

p (5) = (5)³ – 3 (5)² – 9 (5) – 5

= 125 – 75 – 45 – 5 = 0

Therefore, (x – 5) is the factor of p (x)

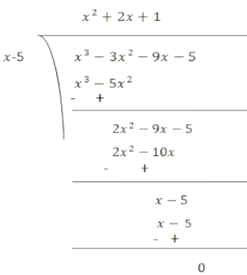
Now, Dividend = Divisor * Quotient + Remainder

(x – 5) (x² + 2x + 1)

= (x – 5) (x² + x + x + 1)

= (x – 5) {x (x + 1) + 1 (x + 1)}= (x – 5) (x + 1) (x + 1)

(iii) Let p (x) = x³ + 13x² + 32x + 20

Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20

By trial method, we find that

p (-1) = 0

So, (x + 1) is factor of p (x)

Now,

p (x) = x³ + 13x² + 32x + 20

p (-1) = (-1)³ + 13 (-1)² + 32 (-1) + 20

= -1 + 13 – 32 + 20 = 0

Therefore, (x + 1) is the factor of p (x)

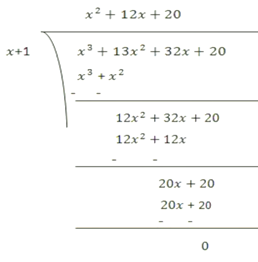
Now, Dividend = Divisor * Quotient + Remainder

(x + 1) (x² + 2x + 20)

= (x + 1) (x² + 2x + 10x + 20)

= (x – 5) {x (x + 2) + 10 (x + 2)}

= (x – 5) (x + 2) (x + 10)

(iv) Let, p(y) = 2y³ + y² – 2y – 1

Factors of ab = 2 * (-1) = -2 are ±1 and ±2

By trial method, we find that

p (1) = 0

So, (y – 1) is a factor of p (y)

Now,

p (y) = 2y³ + y² – 2y – 1

p (1) = 2 (1)³ + (1)² – 2 (1) – 1

= 2 + 1 -1 -1 = 0

Therefore, (y – 1) is the factor if p (y)

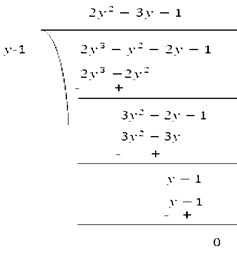
Now, Dividend = Divisor * Quotient + Remainder

(y – 1) (2y² + 3y + 1)

= (y – 1) (2y² + 2y + y + 1)

= (y – 1) {2y (y + 1) + 1 (y + 1)}

= (y – 1) (2y + 1) (y + 1)