What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14)

Question

What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use &pi; = 3.14)

Philoid · Accepted Answer

The diagram is given as:

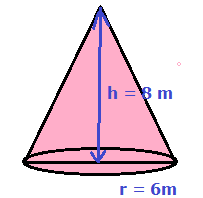
Height (h) = 8m

Radius (r) = 6m

Now, we know that,

According to Pythagoras theorem, l²= r² + h²

⇒ l²= 6² + 8²

⇒ l²= (6² + 8²)

⇒ l²= 36 + 64

⇒ l²= 100

⇒ l = √100 = 10 m

CSA of conical tent = πrl

= π × 6m × 10 m

= 22/7 × 6m × 10 m

= 188.57 m²

≈ 186 m²

Now, Let the length of tarpaulin sheet required be 'x' m

As 20 cm will be wasted, therefore, the effective length will be = (x − 20 cm) = (x − 0.2 m)

Breadth of tarpaulin = 3 m

Area of sheet = CSA of tent

⇒ [(x − 0.2 m) × 3] m = 188.4 m²

⇒ x − 0.2 m = 62.8 m

⇒x = 63 m

Therefore, the length of the required tarpaulin sheet will be 63 m