Obtain all other zeroes of 
if two of its zeroes are
and 
p(x) = 3x4+6x3-2x2-10x-5
Since the two zeroes are 
is a factor of 3x4+6x3-2x2-10x-5
Therefore, we divide the given polynomial by 
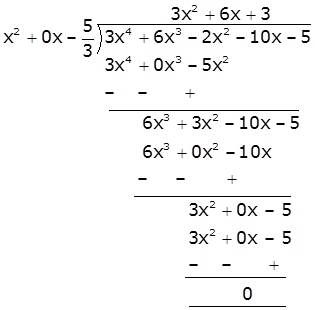
3x4+6x3-2x2-10x-5 = 
= 
we factorize x2+2x+1,
= (x+1)2
Therefore, its zero is given by x + 1 = 0 x = −1
As it has the term (x+1)2, therefore, there will be 2 zeroes at x = −1.
Hence, the zeroes of the given polynomial are 
, −1 and −1.
13