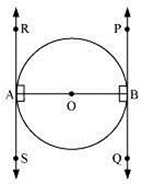
Let AB is diameter of the circle. Two tangents PQ and RS are drawn at points A and B respectively. Radius drawn to these tangents will be perpendicular to the tangents.

Thus, OA ⊥ RS and OB ⊥ PQ

∠OAR = 90°

∠OAS = 90°

∠OBP = 90°

∠OBQ = 90°

It can be observed that

∠OAR = ∠ OBQ (Alternate interior angles)

∠OAS = ∠ OBP (Alternate interior angles)

Since alternate interior angles are equal, lines PQ and RS will be parallel.