The lengths of 40 leaves of a plant are measured correct to the nearest milli meter, and the data obtained is represented in the following table:
Length (in mm) | Number of leaves |
118 - 126 127 - 135 136 - 144 145 - 153 154 - 162 163 - 171 172 - 180 | 3 5 9 12 5 4 2 |
Find the median length of the leaves
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5)
The cumulative frequency of the data can be calculated as:
Class interval | frequency | Cumulative frequency |
117.5-126.5 | 3 | 3 |
126.5-135.5 | 5 | 8 |
135.5-144.5 | 9 | 17 |
144.5-153.5 | 12 | 29 |
153.5-162.5 | 5 | 34 |
162.5-171.5 | 4 | 38 |
171.5-180.5 | 2 | 40 |
As per the question,
N= 40
![]()
Hence,
Median class =144.5-153.5
Lower limit, l = 144.5
cf = 17
f = 12
h = 9
Now,
Median can be calculated as:
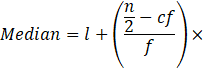
![]()
= 144.5 + ![]()
= 146.75