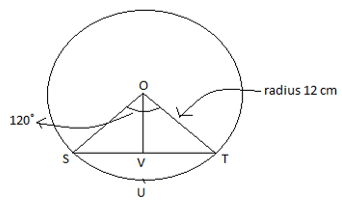
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle (Use π = 3.14 and √3 = 1.73)

Question

A chord of a circle of radius 12 cm subtends an angle of 120&deg; at the centre. Find the area of the corresponding segment of the circle (Use &pi; = 3.14 and &radic;3 = 1.73)

Philoid · Accepted Answer

Let us draw a perpendicular OV on chord ST. It will bisect the chord ST and the angle O.

SV = VT

In ΔOVS,

= Cos 60^o

=

OV = 6 cm

= Sin 60^o

=

SV = 6√3 cm

ST = 2 * SV

= 2 * 6√3

= 12√3 cm

Area of ΔOST = * 12√3 * 6

= 36√3

= 36 * 1.73

= 62.28 cm²

Area of sector OSUT = * π * (12)²

= * 3.14 * 144

= 150.72 cm²

Area of segment SUT = Area of sector OSUT - Area of ΔOST

= 150.72 - 62.28

= 88.44 cm²

A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle(Use π = 3.14 and √3 = 1.73)

A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle

(Use π = 3.14 and √3 = 1.73)