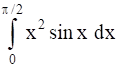
We are asked to calculate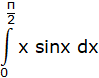

For this we have to apply integration by parts

Let u and v be two functions then

To choose the first function u we use “ILATE” rule

That is

I=inverse trigonometric function

L=logarithmic function

A=algebraic function

T=trigonometric functions

E=exponential function

So in this preference, the first function is choosen to make the integration simpler.

Now, In the given question x is an algebraic function and it is chosen as u (A comes first in “ILATE” rule)

So first let us integrate the equation and then let us substitute the limits in it

Therefore, now substitute the limits given:

Note that and

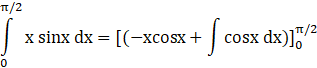
First we have to substitute the upper limit and then subtract the second limit value from it
)

Note that sin0= 0 and cos0=1

=0+1+0–0

=1