Evaluate the following Integrals:
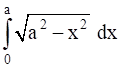
Given Definite Integral can be written as:
![]() …… (1)
…… (1)
Let us assume x = a sinθ
Differentiating w.r.t x on both sides we get,
⇒ d(x) = d(a sin θ)
⇒ dx = a cos θ dθ ……(2)
Let us find the value of ![]()
![]()
![]()
![]()
(∵ 1 – sin2θ = cos2θ)
![]() ……(3)
……(3)
Lower limit for the Definite Integral:
![]()
⇒ θ = sin-1(0)
⇒ θ = 0……(4)
Upper limit for the Definite Integral:
![]()
⇒ θ = sin-1(1)
![]() ……(5)
……(5)
Substituting (2),(3),(4),(5) in eq(1) we get,
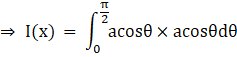
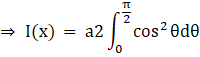
We know that cos2θ = 2cos2θ – 1
Then
![]()
Using these result for the integration, we get,
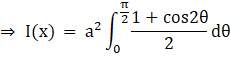
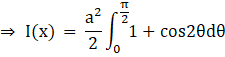
We know that:
∫ adx = ax + c and also
![]()
We know that:
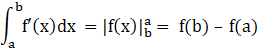
[here f’(x) is derivative of f(x)).
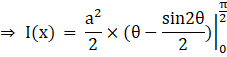
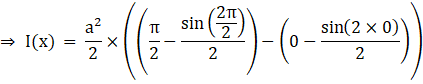
We know that sinnπ = 0 (n∈I)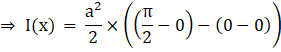
![]()
![]()
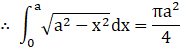
10