Evaluate the following Integrals:
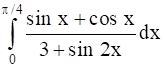
Let ![]()
In the denominator, we have sin 2x = 2 sin x cos x
Note that we can write 2 sin x cos x = 1 – (1 – 2 sin x cos x)
We also have sin2x + cos2x = 1
⇒ 1 – 2 sin x cos x = sin2x + cos2x – 2 sin x cos x
⇒ sin 2x = 1 – (sin x – cos x)2
So, using this, we can write our integral as
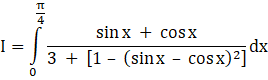
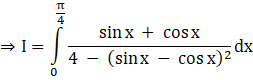
Now, put sin x – cos x = t
⇒ (cos x + sin x) dx = dt (Differentiating both sides)
When x = 0, t = sin 0 – cos 0 = 0 – 1 = -1
When,
![]()
So, the new limits are -1 and 0.
Substituting this in the original integral,
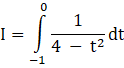
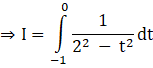
Recall,
![]()
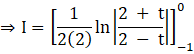
![]()
![]()
![]()
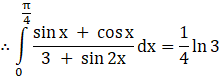
31