Evaluate the following Integrals:
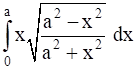
Let ![]()
As we have the trigonometric identity
![]()
to evaluate this integral we use x2 = a2cos 2θ
⇒ 2xdx = –2a2sin(2θ)dθ (Differentiating both sides)
⇒ xdx = –a2sin(2θ)dθ
![]()
![]()
When x = a, a2cos 2θ = a2⇒ cos 2θ = 1
⇒ 2θ = 0 ⇒ θ = 0
So, the new limits are ![]() and 0.
and 0.
Also,
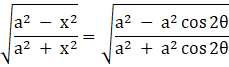
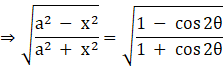
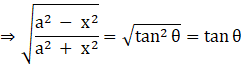
Substituting this in the original integral,
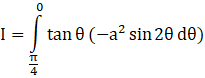
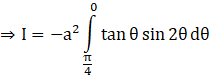
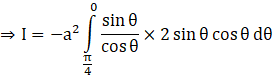
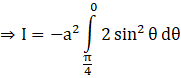
But, we have 2 sin2θ = 1 – cos 2θ
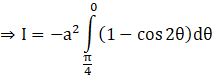
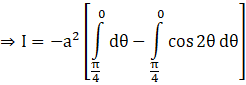
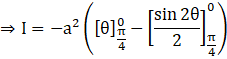
![]()
![]()
![]()
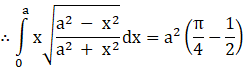
54