Show that y = ae2x + be–x is a solution of the differential equation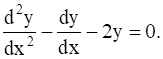
The differential equation is ![]() and the function that is to be proven as solution is
and the function that is to be proven as solution is
y = ae2x + be–x, now we need to find the value of ![]() and
and ![]() .
.
![]() = 2ae2x – be–x
= 2ae2x – be–x
![]() = 4ae2x + be–x
= 4ae2x + be–x
Putting these values in the equation, we get,
4ae2x + be–x –(2ae2x – be–x) – 2(ae2x + be–x) = 0,
0 = 0
As, L.H.S = R.H.S. the equation is satisfied, so hence this function is the solution of the differential equation.
3