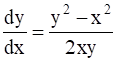
Given differential equation can be written as:

⇒ ……(1)

Homogeneous equation: A equation is said to be homogeneous if f(zx,zy) = zⁿf(x,y) (where n is the order of the homogeneous equation).

Let us assume:

⇒

⇒

⇒

⇒ f(zx,zy) = z⁰f(x,y)

So, given differential equation is a homogeneous differential equation.

We need a substitution to solve this type of linear equation and the substitution is y = vx.

Let us substitute this in (1)

⇒

We know that:

⇒

⇒

⇒

⇒

⇒

Bringing like variables on one side we get,

⇒

⇒

We know that:

Integrating on both sides, we get,

⇒

⇒ log(v² + 1) = -logx + logC (∵ LogC is an arbitrary constant)

Since y = vx,

we get

⇒

(∵ )

Applying exponential on both sides, we get,

⇒

⇒

Cross multiplying on both sides we get,

⇒ y² + x² = Cx

∴ The solution for the given differential equation is y² + x² = Cx.